537. Erect the Fence

here are some trees, where each tree is represented by (x,y) coordinate in a two-dimensional garden. Your job is to fence the entire garden using theminimum lengthof rope as it is expensive. The garden is well fenced only if all the trees are enclosed. Your task is to help find the coordinates of trees which are exactly located on the fence perimeter.

Example 1:

Input:
 [[1,1],[2,2],[2,0],[2,4],[3,3],[4,2]]

Output:
 [[1,1],[2,0],[4,2],[3,3],[2,4]]

Explanation:

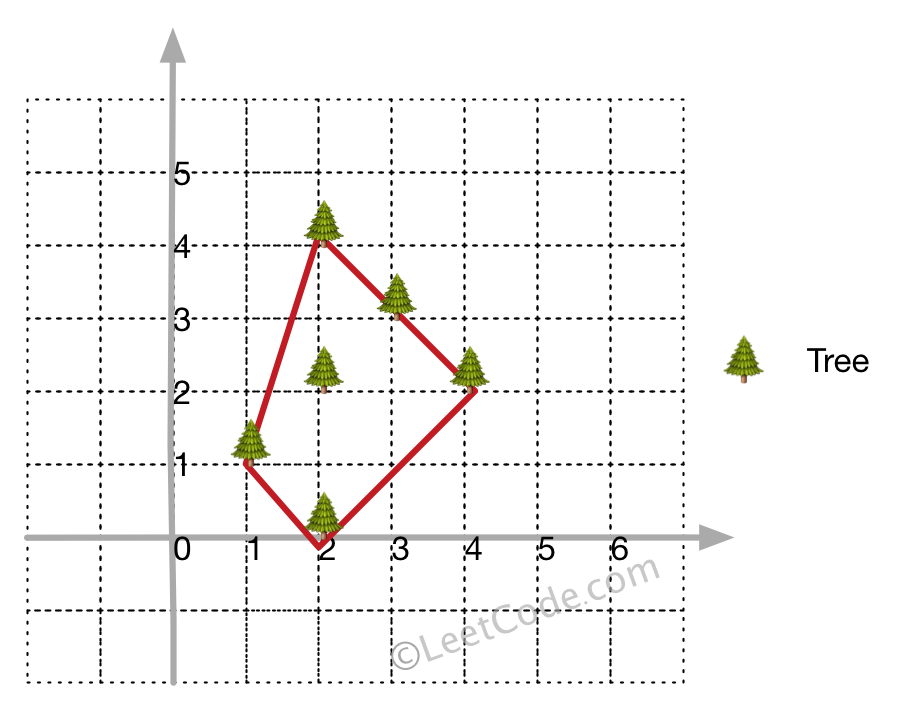Example 2:

Input:
 [[1,2],[2,2],[4,2]]

Output:
 [[1,2],[2,2],[4,2]]

Explanation:

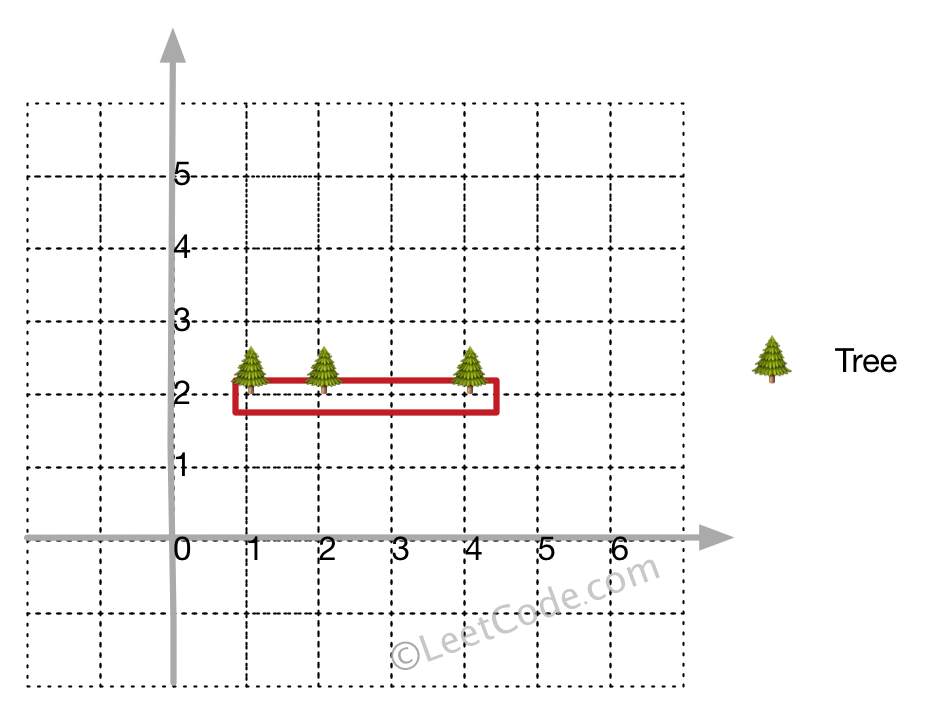
Even you only have trees in a line, you need to use rope to enclose them.

Note:

1. All trees should be enclosed together. You cannot cut the rope to enclose trees that will separate them in more than one group.
2. All input integers will range from 0 to 100.
3. The garden has at least one tree.
4. All coordinates are distinct.
5. Input points have NO order. No order required for output.

Thoughts:

1. Find the next convex "base" point, expand the co-linear points with it by using the Cross Product. (reason)
2. Repeat doing this until the graph traverses back to the original point.
3. This is essentially Jarvis'algorithm (or wrapping) with co-linear checks. (Other ways to solve convex Hull include Graham Scan, Simple Divide and Conquer Algorithm, and )
4. Time Complexity of three Algorithm: | Jarvis | Graham Scan | Andrew's Monotone Chain | Divide and Conquer | | :--- | :--- | :--- | :--- | | O(n^2) | O(nlogn) | O(nlogn) | O(n^3) |

Note: Cross Product = 0 <=> 1. there is a zero vector (current point reaches the base point) 2. two vectors are parallel (or anti-parallel, the angle between is either 0 or 180 degree)

Code Monotone Chain:

1. sort points based on the x value as first priority, then y value
2. build the lower hull: compare the cross product of second_last, last and current point, if negative, means the
previous vec made the clockwise turn, at which we should get rid of the last value as it is not a eligible vertex.
3. build the upper hull: repeat the step 2 with reversely traversing the vector.

class Solution {
public:
    int orientation(Point &p, Point &q, Point &r) {
        return (q.y - p.y) * (r.x - q.x) - (q.x - p.x) * (r.y - q.y);
    }

    vector<Point> outerTrees(vector<Point>& points) {
        if (points.size() <= 3)
            return points;

        //sort lexicographically
        sort(points.begin(), points.end(), [](Point &p, Point &q) {
            return p.x < q.x || (p.x == q.x && p.y < q.y);
        });

        vector<Point> ans;

        //lower hull 
        for (int i = 0; i < points.size(); ++i) {
            while (ans.size() >= 2 && orientation(ans[ans.size() - 2], ans[ans.size() - 1], points[i]) < 0)
                ans.pop_back();
            ans.push_back(points[i]);
        }
        // remove the last point as it will be included in the upper hull
        ans.pop_back();

        // upper hull
        for (int i = points.size() - 1; i >= 0; --i) {
            while (ans.size() >= 2 && orientation(ans[ans.size() - 2], ans[ans.size() - 1], points[i]) < 0)
                ans.pop_back();
            ans.push_back(points[i]);
        }

        // remove the last point as it was included as the first point explored;
        ans.pop_back();
        return ans;
    }
};

Other two comparable solutions: 1, 2.

1. class Solution {
   public:
       vector<Point> outerTrees(vector<Point>& points) {
           // Andrew's monotone chain method
           int n = points.size();
           vector<Point> ans;
           sort(points.begin(), points.end(), mycompare);
           // left to right
           for (int i = 0; i < n; ++i) {
               while (ans.size() > 1 && orientation(ans[ans.size()-2], ans.back(), points[i]) < 0) 
                   ans.pop_back();
               ans.push_back(points[i]);
           }
           // if all points along a line, ans.size() is n after left to right procedure
           if (ans.size() == n) return ans;
           // right to left
           for (int i = n-2; i >= 0; --i) {
               while (ans.size() > 1 && orientation(ans[ans.size()-2], ans.back(), points[i]) < 0) 
                   ans.pop_back();
               ans.push_back(points[i]);
           }
           ans.pop_back();
           return ans;
       }
   private:
       static bool mycompare(Point& a, Point& b) {
           return a.x < b.x || (a.x == b.x && a.y < b.y);
       }
       int orientation(Point& a, Point& b, Point& c) {
           return (b.x-a.x)*(c.y-b.y) - (b.y-a.y)*(c.x-b.x);
       }
   };
   

     vector<Point> outerTrees(vector<Point>& points) {
        if(points.size() < 3) return points;
        auto cmp = [](Point& a, Point& b) -> bool {
            return a.x < b.x || (a.x == b.x && a.y < b.y);
        };
        sort(points.begin(), points.end(), cmp);
        vector<Point> stack;
        stack.push_back(points[0]);
        stack.push_back(points[1]);
        //left to right;
        for(int i = 2; i < points.size(); ++i) {
            while(stack.size() > 1) {
                auto &t1 = stack.back();
                auto &t2 = stack[stack.size() - 2];
                if(isRightTurn(t2, t1, points[i])) break;
                else stack.pop_back();
            }
            stack.push_back(points[i]);
        }
        int n = stack.size();
        if(n == points.size()) return stack; //check if linear
        stack.push_back(points[points.size() - 2]);
        //right to left;
        for(int i = points.size() - 3; i >= 0; --i) {
            while(stack.size() > n) {
                auto &t1 = stack.back();
                auto &t2 = stack[stack.size() - 2];
                if(isRightTurn(t2, t1, points[i])) break;
                else stack.pop_back();
            }
            stack.push_back(points[i]);
        }
        stack.pop_back();
        return stack;
    }

    bool isRightTurn(Point &a, Point &b, Point &c) {
        return (b.x - a.x) * (c.y - a.y) - (b.y - a.y) * (c.x - a.x) <= 0;
    }

Code Monotone Chain (Python):

def outerTrees(self, A):
    def sign(p, q, r):
        return cmp((p.x - r.x)*(q.y - r.y), (p.y - r.y)*(q.x - r.x))

    def drive(hull, r):
        hull.append(r)
        while len(hull) >= 3 and sign(*hull[-3:]) < 0:
            hull.pop(-2)
        return hull

    A.sort(key = lambda p: (p.x, p.y))
    lower = reduce(drive, A, [])
    upper = reduce(drive, A[::-1], [])
    return list(set(lower + upper))

Code Graham Scan:

1)Find the bottom-most point by comparing y coordinate of all points. If there are two points with same y value, then the point with smaller x coordinate value is considered. Let the bottom-most point be P0. Put P0 at first position in output hull.
2)Consider the remaining n-1 points and sort them by polor angle in counterclockwise order around points[0]. If polor angle of two points is same, then put the nearest point first.
3After sorting, check if two or more points have same angle. If two more points have same angle, then remove all same angle points except the point farthest from P0. Let the size of new array be m.
4)If m is less than 3, return (Convex Hull not possible)
5)Create an empty stack ‘S’ and push points[0], points[1] and points[2] to S.
6)Process remaining m-3 points one by one. Do following for every point ‘points[i]’
4.1)Keep removing points from stack while
orientation
of following 3 points is not counterclockwise (or they don’t make a left turn).
            a) Point next to top in stack
            b) Point at the top of stack
            c) points[i]
4.2)Push points[i] to S
5)Print contents of S

/**
 * Definition for a point.
 * struct Point {
 *     int x;
 *     int y;
 *     Point() : x(0), y(0) {}
 *     Point(int a, int b) : x(a), y(b) {}
 * };
 */
class Solution {


    struct pointsComparator{
        Point p0;
        bool operator() (const Point & p1, const Point& p2){
            int o = orientation(p0, p1, p2);
            if(o == 0) return distSq(p0, p2)>= distSq(p0, p1);
            return o == 2;
        }

        pointsComparator(Point p): p0(p){}
    };
//     int compare(const void *vp1, const void *vp2){
//         Point *p1 = (Point *) vp1;
//         Point *p2 = (Point *) vp2;
//     }

    static int distSq(Point p1, Point p2) {
        return (p1.x - p2.x) * (p1.x - p2.x) + (p1.y - p2.y) * (p1.y - p2.y);
    }

   static int orientation(Point a, Point b, Point c){
        int val = (b.x - a.x)*(c.y-b.y) - (b.y - a.y)*(c.x - b.x);
        if(val == 0) return 0;
        return (val > 0)? 2:1;
    }

    // Point nextTotop(stack<Point> &s){
    //     Point p = s.top();
    //     s.pop();
    //     Point res = s.top();
    //     s.push(p);
    //     return res;
    // }

    // void swap(Point &p1, Point& p2){
    //      Point temp = p1;
    //      p1 = p2;
    //      p2 = temp;
    // }
public:
  vector<Point> outerTrees(vector<Point> points) {
        int n = points.size();
        if (n <= 3) {
            return points;
        }
        // Find the bottommost point
        int ymin = points[0].y, min = 0;
        for (int i = 1; i < n; i++) {
            int y = points[i].y;
            // Pick the bottom-most or chose the left most point in case of tie
            if ((y < ymin) || (ymin == y && points[i].x < points[min].x)) {
                ymin = points[i].y, min = i;
            }
        }

        // Place the bottom-most point at first position
        Point temp = points[0];
        points[0] = points[min];
        points[min] = temp;

        // Sort n-1 points with respect to the first point.
        // A point p1 comes before p2 in sorted ouput 
        // if p2 has larger polar angle (in counterclockwise direction) than p1
        // In the tied case, the one has smaller distance from p0 comes first
        Point p0 = points[0];
        sort(points.begin(), points.end(), pointsComparator(p0));
        //As we need to output all the vertices instead of extreme points
        //We need to sort the points with the same largest polar angle w.r.p. p0 in another way to break tie
        //Closer one comes last
        Point pn = points.back();        
        if (orientation(p0, points[1], pn) != 0) {
            int idx = n-1;
            while (orientation(p0, points[idx], pn) == 0) {
                idx--;
            }
            reverse(points.begin() + idx + 1, points.end());
        }

        // Create an empty stack and push first three points to it.
        vector<Point> vertices;
        vertices.push_back(points[0]);
        vertices.push_back(points[1]);
        vertices.push_back(points[2]);
        // Process remaining n-3 points
        for (int i = 3; i < n; i++) {
            // Keep removing top while the angle formed by
            // points next-to-top, top, and points[i] makes a right (in clockwise) turn
            while (orientation(vertices[vertices.size() - 2], vertices.back(), points[i]) == 1) {
                vertices.pop_back();
            }
            vertices.push_back(points[i]);
        }
        return vertices;
    }

};

Code Javis's Algorithm (Java)

public class Solution {
    public List<Point> outerTrees(Point[] points) {
        Set<Point> result = new HashSet<>();

        // Find the leftmost point
        Point first = points[0];
        int firstIndex = 0;
        for (int i = 1; i < points.length; i++) {
            if (points[i].x < first.x) {
                first = points[i];
                firstIndex = i;
            }
        }
        result.add(first);

        Point cur = first;
        int curIndex = firstIndex;
        do {
            Point next = points[0];
            int nextIndex = 0;
            for (int i = 1; i < points.length; i++) {
                if (i == curIndex) continue;
                int cross = crossProductLength(cur, points[i], next);
                if (nextIndex == curIndex || cross > 0 ||
                        // Handle collinear points
                        (cross == 0 && distance(points[i], cur) > distance(next, cur))) {
                    next = points[i];
                    nextIndex = i;
                }
            }
            // Handle collinear points
            for (int i = 0; i < points.length; i++) {
                if (i == curIndex) continue;
                int cross = crossProductLength(cur, points[i], next);
                if (cross == 0) {
                    result.add(points[i]);
                }
            }

            cur = next;
            curIndex = nextIndex;

        } while (curIndex != firstIndex);

        return new ArrayList<Point>(result);
    }

    private int crossProductLength(Point A, Point B, Point C) {
        // Get the vectors' coordinates.
        int BAx = A.x - B.x;
        int BAy = A.y - B.y;
        int BCx = C.x - B.x;
        int BCy = C.y - B.y;

        // Calculate the Z coordinate of the cross product.
        return (BAx * BCy - BAy * BCx);
    }

    private int distance(Point p1, Point p2) {
        return (p1.x - p2.x) * (p1.x - p2.x) + (p1.y - p2.y) * (p1.y - p2.y);
    }
}

Special Thanks to shawngao's solution and solution by GeeksforGeeks, lee215 and aeonaxx for providing Monotone Chain Solution and equivalent Python solution by awice, along with alternative solution 1 by zestypanda, and 2 by hwf.