218. The Skyline Problem
A city's skyline is the outer contour of the silhouette formed by all the buildings in that city when viewed from a distance. Now suppose you are given the locations and height of all the buildings as shown on a cityscape photo (Figure A), write a program to
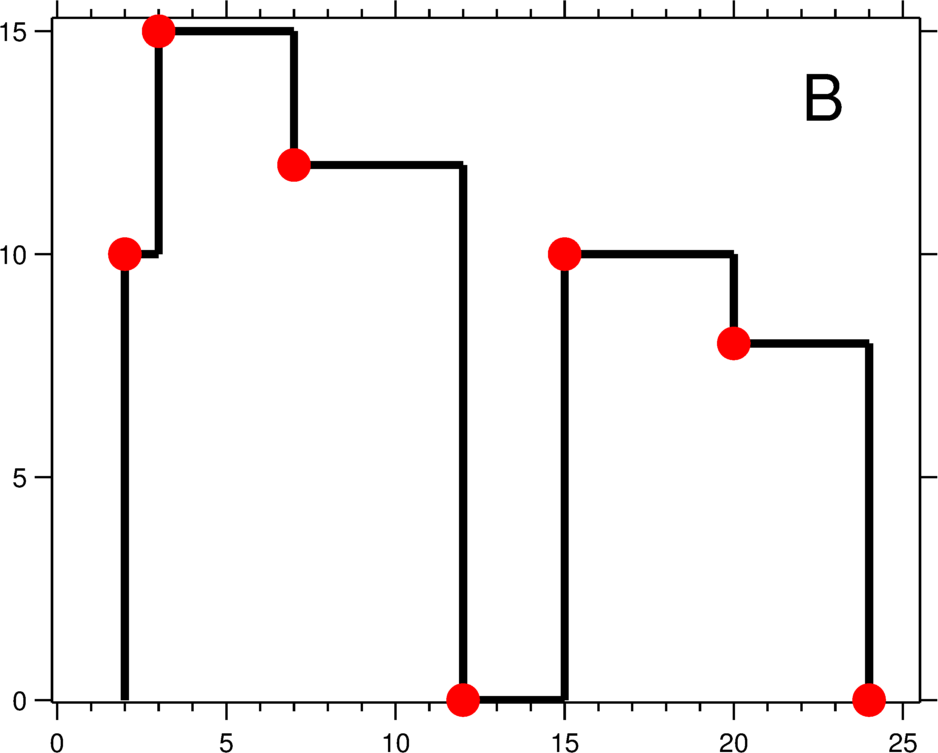
output the skyline formed by these buildings collectively (Figure B).
 The geometric information of each building is represented by a triplet of integers
The geometric information of each building is represented by a triplet of integers[Li, Ri, Hi], whereLiandRiare the x coordinates of the left and right edge of the ith building, respectively, andHiis its height. It is guaranteed that0 ≤ Li, Ri ≤ INT_MAX,0 < Hi ≤ INT_MAX, andRi - Li > 0. You may assume all buildings are perfect rectangles grounded on an absolutely flat surface at height 0.
For instance, the dimensions of all buildings in Figure A are recorded as:[ [2 9 10], [3 7 15], [5 12 12], [15 20 10], [19 24 8] ].
The output is a list of "key points" (red dots in Figure B) in the format of[ [x1,y1], [x2, y2], [x3, y3], ... ]that uniquely defines a skyline.A key point is the left endpoint of a horizontal line segment. Note that the last key point, where the rightmost building ends, is merely used to mark the termination of the skyline, and always has zero height. Also, the ground in between any two adjacent buildings should be considered part of the skyline contour.
For instance, the skyline in Figure B should be represented as:[ [2 10], [3 15], [7 12], [12 0], [15 10], [20 8], [24, 0] ].
Notes:
- The number of buildings in any input list is guaranteed to be in the range
[0, 10000]. - The input list is already sorted in ascending order by the left x position
Li. - The output list must be sorted by the x position.
- There must be no consecutive horizontal lines of equal height in the output skyline. For instance,
[...[2 3], [4 5], [7 5], [11 5], [12 7]...]is not acceptable; the three lines of height 5 should be merged into one in the final output as such:[...[2 3], [4 5], [12 7], ...]
Thoughts:
- Pseudo Algorithm: Our final solution, then, in O(nlogn) time, is as follows. First, sort the critical points. Then scan across the critical points from left to right. When we encounter the left edge of a rectangle, we add that rectangle to the heap with its height as the key. When we encounter the right edge of a rectangle, we remove that rectangle from the heap. (This requires keeping external pointers into the heap.) Finally, any time we encounter a critical point, after updating the heap we set the height of that critical point to the value peeked from the top of the heap. from Brian Gordon's blog
dong.wang.1694's solution: The idea is to do line sweep and just process the buildings only at the start and end points. The key is to use a priority queue to save all the buildings that are still "alive". The queue is sorted by its height and end time (the larger height first and if equal height, the one with a bigger end time first). For each iteration, we first find the current process time, which is either the next new building start time or the end time of the top entry of the live queue. If the new building start time is larger than the top one end time, then process the one in the queue first (pop them until it is empty or find the first one that ends after the new building); otherswise, if the new building starts before the top one ends, then process the new building (just put them in the queue). After processing, output it to the resulting vector if the height changes. Complexity is the worst case O(NlogN). Not sure why my algorithm is so slow considering others' Python solution can achieve 160ms, any commments? here's the probable explanation.
Detailed Implementation from the post by StefanPochmann: a Python version with modification from dong.wang.1694's brilliant C++ solution. It sweeps from left to right. But it doesn't only keepheights_of "alive buildings" in the priority queue and it doesn't remove them as soon as their building is left behind. Instead, (height, right)_pairs_are kept in the priority queue and they stay in there as long as there's a larger height in there, not just until their building is left behind. In each loop, we first check what has the smaller x-coordinate: adding the next building from the input, or removing the next building from the queue. In case of a tie, adding buildings wins, as that guarantees correctness (think about it :-). We then either add all input buildings starting at that x-coordinate or we remove all queued buildings ending at that x-coordinate_or earlier(remember we keep buildings in the queue as long as they're "under the roof" of a larger actually alive building). And then, if the current maximum height in the queue differs from the last in the skyline, we add it to the skyline.
Code Python from StefanPochmann
from heapq import *
class Solution:
def getSkyline(self, LRH):
skyline = []
i, n = 0, len(LRH)
liveHR = []
while i < n or liveHR:
if not liveHR or i < n and LRH[i][0] <= -liveHR[0][1]:
x = LRH[i][0]
while i < n and LRH[i][0] == x:
heappush(liveHR, (-LRH[i][2], -LRH[i][1]))
i += 1
else:
x = -liveHR[0][1]
while liveHR and -liveHR[0][1] <= x:
heappop(liveHR)
height = len(liveHR) and -liveHR[0][0]
if not skyline or height != skyline[-1][1]:
skyline += [x, height],
return skyline
Fastest Python Solution:
class Solution(object):
def getSkyline(self, buildings):
"""
:type buildings: List[List[int]]
:rtype: List[List[int]]
"""
if len(buildings) == 0:
return []
import heapq
h = []
arr = []
lower = buildings[0][0]
def get_height():
return 0 if len(h) == 0 else -h[0][0]
for x1, x2, y in buildings:
if y == 0:
continue
while h and h[0][1] < x1:
a, b = heapq.heappop(h)
if b > lower:
arr.append([lower, -a])
lower = b
if lower < x1 and get_height() < y:
arr.append([lower, get_height()])
lower = x1
while get_height() == y:
x2 = max(x2, heapq.heappop(h)[1])
heapq.heappush(h, (-y, x2))
while h:
a, b = heapq.heappop(h)
if b > lower:
arr.append([lower, -a])
lower = b
arr.append([lower, 0])
return arr
Code from Java: using segments with Priority Queue to solve the problem:
class Solution {
public List<int[]> getSkyline(int[][] buildings) {
List<int[]> heights = new ArrayList<>();
for(int []b : buildings){
// adding two tuples, one with negative (rising edge) height
// and the other with positive (falling edge)
heights.add(new int [] {b[0], -b[2]});
heights.add(new int [] {b[1], b[2]});
}
Collections.sort(heights, (a,b)-> a[0] != b[0]?
a[0] - b[0]:
a[1] - b[1]
);
// max heap for heights
Queue<Integer> pq = new PriorityQueue<>((a,b)->(b-a));
pq.offer(0); // insert 0 to prevent later buildinga from being poped out before right edges come
int prev = 0;
List<int[]> result = new ArrayList<>();
for (int []h : heights){
if(h[1]< 0){
pq.offer(-h[1]);
}
else{
pq.remove(h[1]);
}
// check if top value in the pq is the critical point by checking whether there is a height change
// using prev and current value
int cur = pq.peek();
if(prev!= cur){
result.add(new int[]{h[0], cur});
prev = cur;
}
}
return result;
}
}